§5. Ранг матриці та способи його обчислення

Число r називається рангом матриці A якщо:
1) в матриці A є мінор порядку r відмінний від нуля;
2) всі мінори порядку (r+1) і вище, якщо вони існують, дорівнюють нулю.
Інакше ранг матриці – це найвищий порядок мінору, відмінного від нуля.
Позначення: rangA, r A або r.
З визначення слідує, що r – ціле додатне число. Для нуль-матриці вважають ранг рівним нулю.

Призначення сервісу. Онлайн-калькулятор призначений для знаходження рангу матриці. При цьому рішення зберігається у форматі Word та Excel. див. приклад рішення.

Інструкція. Виберіть розмір матриці, натисніть Далі.

Визначення. Нехай дана матриця рангу r. Будь-який мінор матриці, відмінний від нуля і має порядок r, називається базисним, а рядки та стовпці його складові – базовими рядками та стовпцями.
Відповідно до цього визначення, матриця A може мати кілька базисних мінорів.

Ранг одиничної матриці E дорівнює n (кількості рядків).

Приклад 1 . Дано дві матриці , та їхні мінори , . Який з них можна прийняти як базисний?
Рішення. Мінор M 1 =0, тому він не може бути базовим для жодної з матриць. Мінор M 2 =-9≠0 і має порядок 2, значить його можна прийняти як базисні матриці A або / і B за умови, що вони мають ранги, рівні 2 . Оскільки detB=0 (як визначник з двома пропорційними стовпцями), то rangB=2 і M 2 можна взяти за базисний мінор матриці B. Ранг матриці A дорівнює 3, тому що detA=-27≠0 і, отже, порядок базисного мінору цієї матриці повинен дорівнювати 3, тобто M 2 не є базисним для матриці A . Зазначимо, що у матриці A єдиний базисний мінор, що дорівнює визначнику матриці A .

Теорема (про базисний мінор). Будь-який рядок (стовпчик) матриці є лінійною комбінацією її базисних рядків (стовпців).
Наслідки з теореми.

1. Будь-які (r+1) стовпчиків (рядків) матриці рангу r лінійно залежні.
2. Якщо ранг матриці менший за кількість її рядків (стовпців), то її рядки (стовпці) лінійно залежні. Якщо rangA дорівнює числу її рядків (стовпців), то рядки (стовпці) лінійно незалежні.
3. Визначник матриці A дорівнює нулю і тоді, коли її рядки (стовпці) лінійно залежні.
4. Якщо до рядка (стовпця) матриці додати інший рядок, (стовпець) помножену на будь-яке число, відмінне від нуля, то ранг матриці не зміниться.
5. Якщо у матриці закреслити рядок (стовпець), що є лінійною комбінацією інших рядків (стовпців), то ранг матриці не зміниться.
6. Ранг матриці дорівнює максимальному числу її лінійно незалежних рядків (стовпців).
7. Максимальна кількість лінійно незалежних рядків збігається з максимальною кількістю лінійно незалежних стовпців.

Приклад 2 . Знайти ранг матриці .
Рішення. Виходячи з визначення рангу матриці, шукатимемо мінор найвищого порядку, відмінний від нуля. Спочатку перетворимо матрицю до більш простого вигляду. Для цього перший рядок матриці помножимо на (-2) і додамо до другого, потім її помножимо на (-1) і додамо до третього.

Ранг матриці є важливою числову характеристику. Найбільш характерним завданням, що вимагає знаходження рангу матриці, є перевірка сумісності системи лінійних рівнянь алгебри. У цій статті ми дамо поняття рангу матриці та розглянемо методи його знаходження. Для кращого засвоєння матеріалу докладно розберемо розв'язання кількох прикладів.

Навігація на сторінці.

Визначення рангу матриці та необхідні додаткові поняття.

Перш ніж озвучити визначення рангу матриці, слід добре розібратися з поняттям мінору, а знаходження мінорів матриці має на увазі вміння обчислення визначника. Отже, рекомендуємо при необхідності згадати теорію статті методи знаходження визначника матриці, властивості визначника.

Візьмемо матрицю А порядку. Нехай k - деяке натуральне число, що не перевищує найменшого з чисел m і n, тобто, .

Визначення.

Мінором k-ого порядкуматриці А називається визначник квадратної матриці порядку , складеної з елементів матриці А , які знаходяться в заздалегідь вибраних k рядках і стовпцях k, причому розташування елементів матриці А зберігається.

Іншими словами, якщо в матриці А викреслити (p-k) рядків і (n-k) стовпців, а з елементів, що залишилися, скласти матрицю, зберігаючи розташування елементів матриці А , то визначник отриманої матриці є мінор порядку k матриці А .

Розберемося з визначенням мінору матриці на прикладі.

Розглянемо матрицю .

Запишемо кілька мінорів першого порядку цієї матриці. Наприклад, якщо ми виберемо третій рядок і другий стовпець матриці А, то нашому вибору відповідає мінор першого порядку . Іншими словами, для отримання цього мінору ми викреслили перший і другий рядки, а також перший, третій і четвертий стовпці з матриці А, а з елемента, що залишився, склали визначник. Якщо ж вибрати перший рядок і третій стовпець матриці А, ми отримаємо мінор .

Проілюструємо процедуру отримання розглянутих мінорів першого порядку
і .

Таким чином, мінорами першого порядку матриці є елементи матриці.

Покажемо кілька мінорів другого порядку. Вибираємо два рядки та два стовпці. Наприклад, візьмемо перший і другий рядки і третій і четвертий стовпець. За такого вибору маємо мінор другого порядку . Цей мінор також можна було скласти викреслюванням з матриці третього рядка А, першого і другого стовпців.

Іншим мінором другого порядку матриці А є.

Проілюструємо побудову цих мінорів другого порядку
і .

Аналогічно можуть бути знайдені мінори третього порядку матриці А. Оскільки в матриці всього три рядки, то вибираємо їх усі. Якщо до цих рядків вибрати три перші стовпці, то отримаємо мінор третього порядку

Він може бути побудований викреслюванням останнього стовпця матриці А .

Іншим мінором третього порядку є

виходить викреслюванням третього стовпця матриці А .

Ось малюнок, що показує побудову цих мінорів третього порядку
і .

Для цієї матриці А мінорів порядку вище третього немає, оскільки .

Скільки існує мінорів k-ого порядку матриці А порядку ?

Число мінорів порядку k може бути розраховане як , де і - Число поєднань з p по k і з n по k відповідно.

Як же побудувати всі мінори порядку k матриці А порядку p на n?

Нам знадобиться безліч номерів рядків матриці та безліч номерів стовпців. Записуємо все поєднання з p елементів по k(вони відповідатимуть рядкам матриці А, що вибираються, при побудові мінора порядку k ). До кожного поєднання номерів рядків послідовно додаємо всі поєднання з n елементів до номерів стовпців. Ці набори поєднань номерів рядків та номерів стовпців матриці А допоможуть скласти всі мінори порядку k .

Розберемо з прикладу.

приклад.

Знайдіть усі мінори другого порядку матриці.

Рішення.

Оскільки порядок вихідної матриці дорівнює 3 на 3, то всього мінорів другого порядку буде .

Запишемо всі поєднання з 3 по 2 номерів рядків матриці А: 1, 2; 1, 3 та 2, 3 . Всі поєднання з 3 по 2 номерів стовпців є 1, 2; 1, 3 та 2, 3 .

Візьмемо перший і другий рядки матриці А . Вибравши до цих рядків перший і другий стовпці, перший і третій стовпці, другий і третій стовпці, отримаємо відповідно мінори

Для першого та третього рядків при аналогічному виборі стовпців маємо

Залишилося до другого та третього рядків додати перший та другий, перший та третій, другий та третій стовпці:

Отже, всі дев'ять мінорів другого порядку матриці знайдено.

Тепер можна переходити до визначення рангу матриці.

Визначення.

Ранг матриці- Це найвищий порядок мінора матриці, відмінного від нуля.

Ранг матриці А позначають як Rank (A). Можна також зустріти позначення Rg(A) або Rang(A).

З визначень рангу матриці і мінора матриці можна зробити висновок, що ранг нульової матриці дорівнює нулю, а ранг ненульової матриці не менше одиниці.

Знаходження рангу матриці за визначенням.

Отже, першим методом знаходження рангу матриці є метод перебору мінорів. Цей спосіб ґрунтується на визначенні рангу матриці.

Нехай нам потрібно знайти ранг матриці А порядку.

Коротко опишемо алгоритмрозв'язання цього завдання способом перебору мінорів.

Якщо є хоча б один елемент матриці, відмінний від нуля, то ранг матриці як мінімум дорівнює одиниці (оскільки є мінор першого порядку, не рівний нулю).

Далі перебираємо мінори другого порядку. Якщо всі мінори другого порядку дорівнюють нулю, то ранг матриці дорівнює одиниці. Якщо існує хоча б один ненульовий мінор другого порядку, переходимо до перебору мінорів третього порядку, а ранг матриці як мінімум дорівнює двом.

Аналогічно, якщо всі мінори третього порядку дорівнюють нулю, то ранг матриці дорівнює двом. Якщо існує хоча б один мінор третього порядку, відмінний від нуля, то ранг матриці як мінімум дорівнює трьом, а ми переступаємо до перебору мінорів четвертого порядку.

Зазначимо, що ранг матриці не може перевищувати найменшого числа p і n .

приклад.

Знайдіть ранг матриці .

Рішення.

Оскільки матриця ненульова, її ранг не менше одиниці.

Мінор другого порядку відмінний від нуля, отже, ранг матриці не менше двох. Переходимо до перебору мінорів третього порядку. Усього їх штук.

Усі мінори третього порядку дорівнюють нулю. Тому ранг матриці дорівнює двом.

Відповідь:

Rank(A) = 2.

Знаходження рангу матриці методом облямівних мінорів.

Існують інші методи знаходження рангу матриці, які дозволяють отримати результат за меншої обчислювальної роботи.

Одним з таких методів є метод облямівних мінорів.

Розберемося з поняттям облямівного мінору.

Кажуть, що мінор М ок (k+1)-ого ​​порядку матриці А облямовує мінор M порядку k матриці А якщо матриця, відповідна мінору М ок , «містить» матрицю, відповідну мінору M .

Інакше кажучи, матриця, відповідна облямовуваному мінору М , виходить з матриці, що відповідає облямівному мінору M ок , викреслюванням елементів одного рядка і одного стовпця.

Наприклад розглянемо матрицю і візьмемо мінор другого порядку. Запишемо всі мінори, що облямовують:

Метод облямівних мінорів обґрунтовується наступною теоремою (наведемо її формулювання без доказу).

Теорема.

Якщо всі мінори, що оздоблюють мінор k-ого порядку матриці А порядку p на n, дорівнюють нулю, то всі мінори порядку (k+1) матриці А дорівнюють нулю.

Таким чином, для знаходження рангу матриці не обов'язково перебирати всі мінори, що досить облямовують. Кількість мінорів, що оздоблюють мінор k-ого порядку матриці А порядку, знаходиться за формулою . Зазначимо, що мінорів, що оздоблюють мінор k-ого порядку матриці А, не більше, ніж мінорів (k + 1)-ого ​​порядку матриці А. Тому, здебільшого використання методу облямівних мінорів вигідніше простого перебору всіх мінорів.

Перейдемо до знаходження рангу матриці методом облямівних мінорів. Коротко опишемо алгоритмцього методу.

Якщо матриця А ненульова, то як мінор першого порядку беремо будь-який елемент матриці А відмінний від нуля. Розглядаємо його мінори, що облямовують. Якщо вони рівні нулю, то ранг матриці дорівнює одиниці. Якщо є хоча б один ненульовий облямівний мінор (його порядок дорівнює двом), то переходимо до розгляду його облямівних мінорів. Якщо вони рівні нулю, то Rank(A) = 2 . Якщо хоча б один оздоблюючий мінор відмінний від нуля (його порядок дорівнює трьом), то розглядаємо його мінори, що облямовують. І так далі. У результаті Rank(A) = k , якщо всі обрамляють мінори (k + 1)-ого ​​порядку матриці А дорівнюють нулю, або Rank(A) = min(p, n) , якщо існує ненульовий мінор, що облямовує мінор порядку (min( p, n) - 1).

Розберемо метод окаймляющих мінорів знаходження рангу матриці з прикладу.

приклад.

Знайдіть ранг матриці методом облямівних мінорів.

Рішення.

Оскільки елемент a 1 1 матриці А відмінний від нуля, то візьмемо його як мінор першого порядку. Почнемо пошук обрамляючого мінору, відмінного від нуля:

Знайдений мінор другого порядку, відмінний від нуля. Переберемо його окаймляющие мінори (їх штук):

Усі мінори, що оздоблюють мінор другого порядку , дорівнюють нулю, отже, ранг матриці А дорівнює двом.

Відповідь:

Rank(A) = 2.

приклад.

Знайдіть ранг матриці за допомогою облямівних мінорів.

Рішення.

Як відмінний від нуля мінор першого порядку візьмемо елемент a 1 1 = 1 матриці А . Мінор другого порядку, який його облямовує не дорівнює нулю. Цей мінор оздоблюється мінором третього порядку
. Так як він не дорівнює нулю і для нього не існує жодного облямівного мінору, то ранг матриці А дорівнює трьом.

Відповідь:

Rank(A) = 3 .

Знаходження рангу з допомогою елементарних перетворень матриці (методом Гауса).

Розглянемо ще один спосіб знаходження рангу матриці.

Наступні перетворення матриці називають елементарними:

• перестановка місцями рядків (або стовпців) матриці;
• множення всіх елементів будь-якого рядка (стовпця) матриці на довільне число k відмінне від нуля;
• додавання до елементів будь-якого рядка (стовпця) відповідних елементів іншого рядка (стовпця) матриці, помножених на довільне число k .

Матриця називається еквівалентної матриці А, якщо отримана з А за допомогою кінцевого числа елементарних перетворень. Еквівалентність матриць позначається символом "~", тобто записується A~B.

Знаходження рангу матриці за допомогою елементарних перетворень матриці засноване на затвердженні: якщо матриця отримана з матриці А за допомогою кінцевого числа елементарних перетворень, то Rank(A) = Rank(B) .

Справедливість цього твердження випливає із властивостей визначника матриці:

• При перестановці рядків (або шпальт) матриці її визначник змінює знак. Якщо він дорівнює нулю, то при перестановці рядків (стовпців) він залишається рівним нулю.
• При множенні всіх елементів якогось рядка (стовпця) матриці на довільне число k відмінне від нуля, визначник отриманої матриці дорівнює визначнику вихідної матриці, помноженого на k . Якщо визначник вихідної матриці дорівнює нулю, то після множення всіх елементів будь-якого рядка або стовпця на число k визначник отриманої матриці також дорівнює нулю.
• Додавання до елементів деякого рядка (стовпця) матриці відповідних елементів іншого рядка (стовпця) матриці, помножених на деяке число k не змінює її визначника.

Суть методу елементарних перетвореньполягає у приведенні матриці, ранг якої нам потрібно знайти, до трапецієподібної (в окремому випадку до верхньої трикутної) за допомогою елементарних перетворень.

Навіщо це робиться? Ранг матриць такого виду легко знайти. Він дорівнює кількості рядків, що містять хоча б один ненульовий елемент. Оскільки ранг матриці під час проведення елементарних перетворень не змінюється, то отримане значення буде рангом вихідної матриці.

Наведемо ілюстрації матриць, одна з яких має вийти після перетворень. Їхній вигляд залежить від порядку матриці.

Ці ілюстрації є шаблонами, яких будемо перетворювати матрицю А .

Опишемо алгоритм методу.

Нехай нам потрібно знайти ранг ненульової матриці А порядку (p може дорівнювати n ).

Отже, . Помножимо всі елементи першого рядка матриці А на . При цьому отримаємо еквівалентну матрицю, позначимо її А (1):

До елементів другого рядка отриманої матриці А (1) додамо відповідні елементи першого рядка, помножені на . До елементів третього рядка додамо відповідні елементи першого рядка, помножені на . І так далі до p-го рядка. Отримаємо еквівалентну матрицю, позначимо її А (2):

Якщо всі елементи отриманої матриці, що знаходяться в рядках з другої по p-у , дорівнюють нулю, то ранг цієї матриці дорівнює одиниці, а отже, і ранг вихідної матриці дорівнює одиниці.

Якщо ж у рядках з другого по p-ий є хоча б один ненульовий елемент, то продовжуємо проводити перетворення. Причому діємо абсолютно аналогічно, але лише із зазначеною на малюнку частиною матриці А (2)

Якщо , то переставляємо рядки та (або) стовпці матриці А (2) так, щоб «новий» елемент став ненульовим.

Визначення. Рангом матриціназивається максимальне число лінійно незалежних рядків, що розглядаються як вектори.

Теорема 1 про ранг матриці. Рангом матриціназивається максимальний порядок відмінного від нуля мінора матриці.

Поняття мінора ми вже розбирали на уроці за визначниками, а зараз узагальнимо його. Візьмемо в матриці скільки рядків і скільки стовпців, причому це "скільки-то" має бути менше числа рядків і стовпців матриці, а для рядків і стовпців це "скільки-то" має бути одним і тим же числом. Тоді на перетині скільки рядків і скільки стовпців виявиться матриця меншого порядку, ніж наша вихідна матриця. Визначник це матриці і буде мінором k-го порядку, якщо згадане "скількись" (кількість рядків і стовпців) позначимо через k.

Визначення.Мінор ( r+1)-го порядку, всередині якого лежить обраний мінор r-го порядку, називається називається облямовуючим для даного мінору.

Найчастіше використовуються два способи відшукання рангу матриці. Це спосіб окаймляючих міноріві спосіб елементарних перетворень(Методом Гауса).

При способі облямівних мінорів використовується наступна теорема.

Теорема 2 про ранг матриці.Якщо з елементів матриці можна скласти мінор r-го порядку, не рівний нулю, то ранг матриці дорівнює r.

При способі елементарних перетворень використовується така властивість:

Якщо шляхом елементарних перетворень отримано трапецієподібну матрицю, еквівалентну вихідній, то рангом цієї матриціє число рядків у ній крім рядків, що повністю складаються з нулів.

Знаходження рангу матриці способом обрамляють мінорів

Облямовуючим мінором називається мінор більшого порядку по відношенню до даного, якщо цей мінорм більшого порядку містить у собі даний мінор.

Наприклад, дана матриця

Візьмемо мінор

оздоблюватимуть такі мінори:

Алгоритм знаходження рангу матрицінаступний.

1. Знаходимо не рівні нулю мінори другого порядку. Якщо всі мінори другого порядку дорівнюють нулю, то ранг матриці дорівнюватиме одиниці ( r =1 ).

2. Якщо існує хоча б один мінор другого порядку, не рівний нулю, то складаємо мінеральні мінори третього порядку. Якщо всі облямівні мінори третього порядку дорівнюють нулю, то ранг матриці дорівнює двом ( r =2 ).

3. Якщо хоча б один з облямовливих мінорів третього порядку не дорівнює нулю, то складаємо мінори, що його облямовують. Якщо всі облямівні мінори четвертого порядку дорівнюють нулю, то ранг матриці дорівнює трьом ( r =2 ).

4. Продовжуємо так, поки дозволяє розмір матриці.

приклад 1.Знайти ранг матриці

.

Рішення. Мінор другого порядку .

Облямовуємо його. Окаймляючих мінорів буде чотири:

,

,

Таким чином, усі обрамляючі мінори третього порядку дорівнюють нулю, отже, ранг даної матриці дорівнює двом ( r =2 ).

приклад 2.Знайти ранг матриці

Рішення. Ранг даної матриці дорівнює 1, так як всі мінори другого порядку цієї матриці дорівнюють нулю (у цьому, як і у випадках обрамляють мінорів у двох наступних прикладах, дорогим студентам пропонується переконатися самостійно, можливо, використовуючи правила обчислення визначників), а серед мінорів першого порядку тобто серед елементів матриці, є не рівні нулю.

Приклад 3.Знайти ранг матриці

Рішення. Мінор другого порядку цієї матриці , у всі мінори третього порядку цієї матриці дорівнюють нулю. Отже, ранг цієї матриці дорівнює двом.

Приклад 4.Знайти ранг матриці

Рішення. Ранг цієї матриці дорівнює 3, так як єдиний мінор третього порядку цієї матриці дорівнює 3.

Знаходження рангу матриці способом елементарних перетворень (методом Гауса)

Вже на прикладі 1 видно, що завдання визначення рангу матриці способом обрамляють мінорів вимагає обчислення великої кількостівизначників. Існує, однак, спосіб, що дозволяє звести обсяг обчислень до мінімуму. Цей спосіб заснований на використанні елементарних перетворень матриць і називається також методом Гауса.

Під елементарними перетвореннями матриці розуміються такі операції:

1) множення будь-якого рядка або якогось стовпця матриці на число, відмінне від нуля;

2) додавання до елементів будь-якого рядка або будь-якого стовпця матриці відповідних елементів іншого рядка або стовпця, помножених на те саме число;

3) зміна місцями двох рядків чи стовпців матриці;

4) видалення "нульових" рядків, тобто таких, всі елементи яких дорівнюють нулю;

5) видалення всіх пропорційних рядків, крім одного.

Теорема.При елементарному перетворенні ранг матриці змінюється. Іншими словами, якщо ми є елементарними перетвореннями від матриці Aперейшли до матриці B, то.

Будь-яка матриця Aпорядку m×nможна розглядати як сукупність mвекторів рядків або nвекторів стовпців.

Рангомматриці Aпорядку m×nназивається максимальна кількість лінійно-незалежних векторів стовпців або векторів рядків.

Якщо ранг матриці Aдорівнює r, То пишеться:

Знаходження рангу матриці

Нехай Aдовільна матриця порядку m× n. Для знаходження рангу матриці Aзастосуємо до неї спосіб виключення Гауса.

Відзначимо, що якщо на якомусь етапі виключення провідний елемент виявиться рівним нулю, то міняємо місцями цей рядок з рядком, в якому провідний елемент відрізняється від нуля. Якщо виявиться, що немає такого рядка, то переходимо до наступного стовпця тощо.

Після прямого ходу виключення Гауса отримаємо матрицю, елементи якої під головною діагоналлю дорівнюють нулю. Крім цього, можуть виявитися нульові вектори рядка.

Кількість ненульових векторів рядків і буде рангом матриці A.

Розглянемо це на простих прикладах.

приклад 1.

Помноживши перший рядок на 4 і додавши до другого рядка та помноживши перший рядок на 2 та додавши до третього рядка маємо:

Другий рядок помножимо на -1 і додамо до третього рядка:

Отримали два ненульові рядки і, отже, ранг матриці дорівнює 2.

приклад 2.

Знайдемо ранг наступної матриці:

Помножимо перший рядок на -2 і додамо до другого рядка. Аналогічно обнулили елементи третього та четвертого рядка першого стовпця:

Обнуливши елементи третього та четвертого рядків другого стовпця додаючи відповідні рядки до другого рядка помноженого на число -1.

Розглянемо матрицю А розміру.

А =
Виділимо в ній рядок стовпців (
).

Визначення 26:Мінором k-го порядку матриці А називається визначник квадратної матриці, що виходить з цієї виділенням у ній.

рядків і стовпців.

Визначення 27:Рангомматриці називається найбільший із порядків, відмінних від нуля, її мінорів, r(A).

Визначення 28:Мінор, порядок якого збігається з рангом називається базисним мінором.

Твердження:

1. Ранг виражається цілим числом.
)

2. r=0,
коли А - нульова.

Елементарні перетворення матриць.

До елементарним перетвореннямматриць відносяться такі:

1) множення всіх елементів будь-якого рядка (стовпця) матриці на те саме число.

2) додавання до елементів будь-якого рядка (стовпця) матриці відповідних елементів іншого рядка (стовпця) помножені на те саме число;

3) перестановка місцями рядків (стовпців) матриці;

4) відкидання нульового рядка (стовпця);

5) заміна рядків матриці відповідними стовпцями.

Визначення 29:Матриці, що виходять одна з іншої, при елементарних перетвореннях називається еквівалентними матрицями, позначаються “ ~“

Основна властивість еквівалентних матриць: Ранги еквівалентних матриць рівні.

Приклад 18:Обчислитиr(A),

Рішення:Перший рядок помножимо поетапно на (-4) (-2)

(-7) і потім додамо відповідно до другого, третього та четвертого рядків.

~

поміняємо місцями другий та четвертий рядки
другий рядок помножимо на (-2) і додамо до четвертого рядка; складемо другий і третій рядки.

складемо третій та четвертий рядки.

~
відкинемо нульовий рядок

~
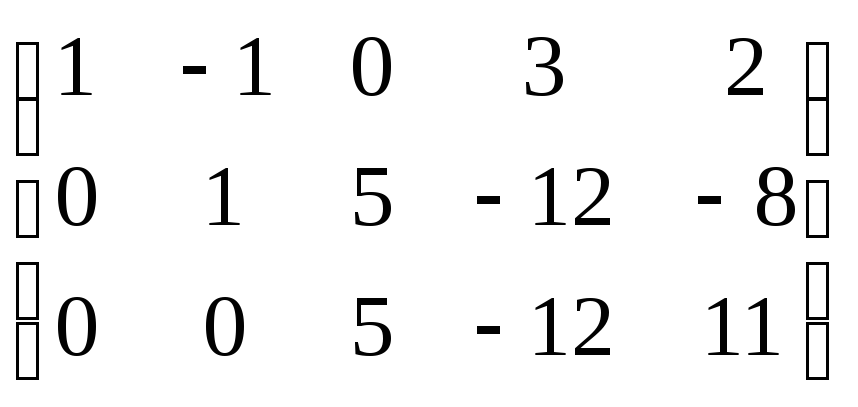r(A)=3
ранг вихідної матриці

дорівнює трьом.

Визначення 30:Назвемо матрицю А ступінчастою, якщо всі елементи головної діагоналі 0, а елементи під головною діагоналлю дорівнюють нулю.

Пропозиція:

1) ранг ступінчастої матриці дорівнює числу її рядків;

2) будь-яка матриця може бути приведена до ступінчастого виду за допомогою елементарних перетворень.

Приклад 19:При яких значеннях  матриця
має ранг, що дорівнює одиниці?

Рішення:Ранг дорівнює одиниці, якщо визначник другого порядку дорівнює нулю, тобто.

§6. Системи лінійних рівнянь загального вигляду.

Система виду
---(9) називається системою загального виду.

Визначення 31:Дві системи називаються рівносильними (еквівалентними), якщо кожне рішення першої системи є другою і навпаки.

У системі (1) матрицю А =
назвемо основною матрицею системи, а =
розширеною матрицею системи

Теорема.Кронекера-Капеллі

Для спільності системи (9) необхідний і достатньо, щоб ранг основної матриці системи дорівнював рангу розширеної матриці, тобто r(A)=r( )

Теорема 1.Якщо ранг матриці спільної системи дорівнює числу невідомих, система має єдине рішення.

Теорема 2.Якщо ранг матриці спільної системи менший за кількість невідомих, то система має безліч рішень.

Правило розв'язання довільної системи лінійних рівнянь:

1)знайти ранги основної та розширеної матриць системи. Якщо
, то система не є спільною.

2) Якщо
=r, то система є спільною. Знайти який-небудь базовий мінор порядку. Базисним називатимемо мінор, на підставі якого визначався ранг матриці.

Невідомі, коефіцієнти яких входять у базисний мінор, називають головними (базисними) і залишають ліворуч, інші ж невідомі називають вільними і переносять праву частину рівняння.

3)Знайти висловлювання головних невідомих через вільні. Отримано загальне рішення системи.

Приклад 20:Дослідити систему та у разі її спільності знайти або єдине чи загальне рішення

Рішення: 1) за Т. Кронекера-Капеллі знаходимо ранги розширеної та основної матриць системи:

~
~

~
~
ранг основної матриці дорівнює двом

2) знаходимо ранг розширеної матриці
~
~
~

3) Висновок:
=2, то система спільна.

Але

система невизначена і має безліч рішень.

4) Базисні невідомі і , Бо вони належать базисному мінору, а - Вільна невідома.

Нехай =с, де с – будь-яке число.

5)Останній матриці відповідає система

6) Відповідь:

7) Перевірка: у будь-яке з рівнянь вихідної системи, де є всі невідомі, підставляємо знайдені значення.